磁場の中を運動する平行平板に加わる力

「電磁気学のベクトル解析」の目次はここをクリック

【問】
　下図のように、紙面に垂直な面の金属の平行平板があり、その両方の金属板を金属線で接続しています。そこに、紙面から紙面の手前に向く磁場（磁束密度Ｂ）を加えます。
　そして、その金属の平行平板を、平板の面の方向で磁場に垂直な方向に速度ｖで運動させます。
　このとき、この金属の平板は電磁場からどのような力を受けるか。
平行平板の面積はＳとし、平行平板の間隔をｄとする。

【解１】
　先ず、この問題を、平行平板といっしょに運動する運動座標系の観測者から観測される状況に基づいて解きます。
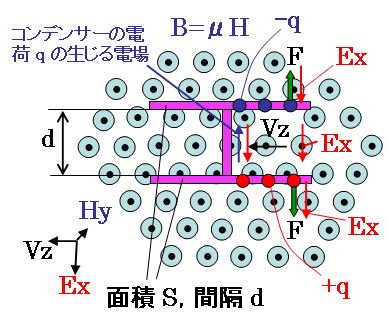
　その座標系で観察すると、下図のように見えます。

　磁場Ｈが速度Ｖｚで運動するので、誘導電場Ｅｘが発生します。

　その誘導電場Ｅｘが加わった金属の平行平板とそれをつなぐ金属線は、どこでも電位が同じになるように電荷が移動して空間から加わった誘導電場Ｅｘを打ち消す電場を発生させます。
　それにより打ち消される金属板間の電圧は、Ｅｘ・ｄです。そのため、平行平板の両端には、平行平板に電圧Ｅｘ・ｄがあらわれるだけの電荷ｑ＝Ｃ・（Ｅｘ・ｄ）がたまります。

　金属の平行平板には電荷ｑがたまりますので、その電荷ｑには、対向する電荷からの電場が加わります。その電場の大きさは以下のように計算できます。

　電荷ｑには、誘導電場Ｅｘと、対向する電荷からの電場とが加わり、その電場の合計が、以下のように、電荷ｑに力Ｆを及ぼします。

この大きさの力Ｆが、平行平板同士を遠ざける方向に加わります。
（解答おわり）

【解２】
　次に、この問題を、磁場と一緒に静止している座標系の観測者の視点で解きます。
（この解き方の方が普通の解き方であると思います）
　その座標系で観察すると、下図のように見えます。

　速度ｖで運動する金属線に、単位長さあたりに起電力Ｅが発生します。金属板間の距離ｄでは、Ｅ・ｄの起電力が発生します。その起電力の電圧Ｅ・ｄが金属板間に加わります。
（磁場中における金属板間の電圧は、観測者の運動座標系が異なれば異なります）
　平行な金属板は容量がＣのコンデンサーを成すので、電圧Ｅ・ｄが加われば、その平行金属板に電荷ｑ＝Ｃ・（Ｅ・ｄ）がたまります。
　そうして溜まった電荷は平行な金属板と一緒に速度ｖで運動しますので、磁場からローレンツ力を、平行平板同士を遠ざける方向に、受けます。

　電荷ｑには、ローレンツ力と、対向する金属板上の電荷の発生する電場（Ｅ／２）からの力を受けます。
　その総和の力を計算すると、以下のようになります。

この大きさの力Ｆが、平行平板同士を遠ざける方向に加わります。
（解答おわり）